ERC-7444: Time Locks Maturity

Abstract

This EIP defines a standardized method to communicate the date on which a time-locked system will become unlocked. This allows for the determination of maturities for a wide variety of asset classes and increases the ease with which these assets may be valued.

Motivation

Time-locks are ubiquitous, yet no standard on how to determine the date upon which they unlock exists. Time-locked assets experience theta-decay, where the time remaining until they become unlocked dictates their value. Providing a universal standard to view what date they mature on allows for improved on-chain valuations of the rights to these illiquid assets, particularly useful in cases where the rights to these illiquid assets may be passed between owners through semi-liquid assets such as ERC-721 or ERC-1155.

Specification

The key words "MUST", "MUST NOT", "REQUIRED", "SHALL", "SHALL NOT", "SHOULD", "SHOULD NOT", "RECOMMENDED", "NOT RECOMMENDED", "MAY", and "OPTIONAL" in this document are to be interpreted as described in RFC 2119 and RFC 8174.

Every ERC-7444 compliant contract must implement ERC-165 interface detection

The maturity return parameter should be implemented in the Unix timestamp standard, which has been used widely in solidity. For example, block.timestamp represents the Unix timestamp when a block is mined in 256-bit value.

For singleton implementations on fungible assets, values passed to id SHOULD be ignored, and queries to such implementations should pass in 0x0

Rationale

Universal Maturities on Locked Assets

Locked Assets have become increasingly popular and used in different parts of defi, such as yield farming and vested escrow concept. This has increased the need to formalize and define an universal interface for all these timelocked assets.

Valuation of Locked Assets via the Black-Scholes Model

Locked Assets cannot be valued normally since the value of these assets can be varied through time and many other different factors throughout the locking time. For instance, The Black-Scholes Model or Black-Scholes-Merton model is an example of a suitable model to estimate the theoretical value of asset with the consideration of impact of time and other potential risks.

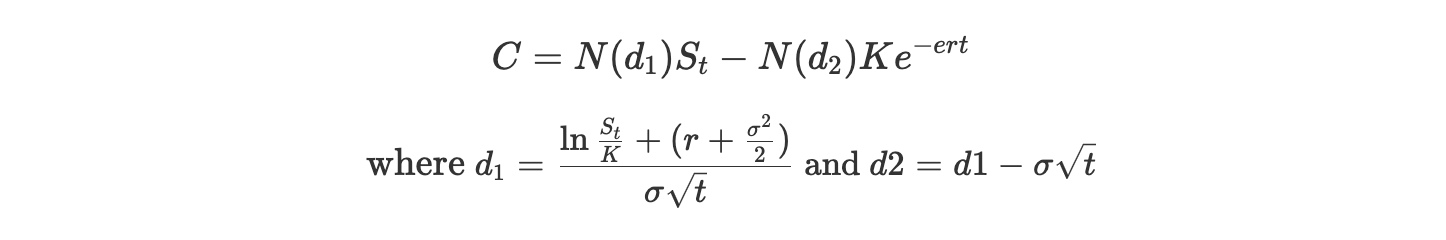
• $C=\text{call option price}$
• $N=\text{CDF of the normal distribution}$
• $S_t=\text{spot price of an asset}$
• $K=\text{strike price}$
• $r=\text{risk-free interest rate}$
• $t=\text{time to maturity}$
• $\sigma=\text{volatility of the asset}$

Time to maturity plays an important role in evaluating the price of timelocked assets, thus the demand to have a common interface for retrieving the data is inevitable.

Backwards Compatibility

This standard can be implemented as an extension to ERC-721 and/or ERC-1155 tokens with time-locked functionality, many of which can be retrofitted with a designated contract to determine the point at which their time locks release.

Reference Implementation

Locked ERC-20 implementation

Security Considerations

Extendable Time Locks

Users or developers should be aware of potential extendable timelocks, where the returned timestamp can be modified through protocols. Users or protocols should check the timestamp carefully before trading or lending with others.

Copyright

Copyright and related rights waived via CC0.