EIP-1283: Net gas metering for SSTORE without dirty maps
In simple terms
What does EIP-1283 do?
EIP-1283 introduces net gas metering for SSTORE operations, tracking original, current, and new values. Operations that don't change the final state (no-ops) cost only 200 gas. Multiple writes to the same slot in a transaction are priced based on net effect rather than each individual operation.
Why is it important?
Before this, each SSTORE cost thousands of gas regardless of final outcome. Net metering makes patterns like reentrancy locks, temporary storage, and repeated updates much cheaper. A lock that's set and cleared in the same transaction costs 400 gas instead of 25,000+.
Metadata
Status: FinalStandards Track: CoreCreated: 2018-08-01
Authors
Wei Tang (@sorpaas)
Abstract
This EIP proposes net gas metering changes for SSTORE opcode, enabling
new usages for contract storage, and reducing excessive gas costs
where it doesn't match how most implementations work.
This acts as an alternative for EIP-1087, where it tries to be friendlier to implementations that use different optimization strategies for storage change caches.
Motivation
This EIP proposes a way for gas metering on SSTORE (as an alternative for EIP-1087 and EIP-1153), using information that is more universally available to most implementations, and requires as little change in implementation structures as possible.
- Storage slot's original value.
- Storage slot's current value.
- Refund counter.
Usages that benefits from this EIP's gas reduction scheme includes:
- Subsequent storage write operations within the same call frame. This includes reentry locks, same-contract multi-send, etc.
- Exchange storage information between sub call frame and parent call frame, where this information does not need to be persistent outside of a transaction. This includes sub-frame error codes and message passing, etc.
Specification
Definitions of terms are as below:
- Storage slot's original value: This is the value of the storage if a reversion happens on the current transaction.
- Storage slot's current value: This is the value of the storage before SSTORE operation happens.
- Storage slot's new value: This is the value of the storage after SSTORE operation happens.
Replace SSTORE opcode gas cost calculation (including refunds) with
the following logic:
- If current value equals new value (this is a no-op), 200 gas is deducted.
- If current value does not equal new value
- If original value equals current value (this storage slot has
not been changed by the current execution context)
- If original value is 0, 20000 gas is deducted.
- Otherwise, 5000 gas is deducted. If new value is 0, add 15000 gas to refund counter.
- If original value does not equal current value (this storage
slot is dirty), 200 gas is deducted. Apply both of the following
clauses.
- If original value is not 0
- If current value is 0 (also means that new value is not 0), remove 15000 gas from refund counter. We can prove that refund counter will never go below 0.
- If new value is 0 (also means that current value is not 0), add 15000 gas to refund counter.
- If original value equals new value (this storage slot is
reset)
- If original value is 0, add 19800 gas to refund counter.
- Otherwise, add 4800 gas to refund counter.
- If original value is not 0
- If original value equals current value (this storage slot has
not been changed by the current execution context)
Refund counter works as before -- it is limited to half of the gas consumed. On a transaction level, refund counter will never go below zero. However, there are some important notes depending on the implementation details:
- If an implementation uses "transaction level" refund counter (refund is checkpointed at each call frame), then the refund counter continues to be unsigned.
- If an implementation uses "execution-frame level" refund counter (a new refund counter is created at each call frame, and then merged back to parent when the call frame finishes), then the refund counter needs to be changed to signed -- at internal calls, a child refund can go below zero.
Explanation
The new gas cost scheme for SSTORE is divided into three different
types:
- No-op: the virtual machine does not need to do anything. This is the case if current value equals new value.
- Fresh: this storage slot has not been changed, or has been reset to its original value. This is the case if current value does not equal new value, and original value equals current value.
- Dirty: this storage slot has already been changed. This is the case if current value does not equal new value, and original value does not equal current value.
We can see that the above three types cover all possible variations of original value, current value, and new value.
No-op is a trivial operation. Below we only consider cases for Fresh and Dirty.
All initial (not-No-op) SSTORE on a particular storage slot starts
with Fresh. After that, it will become Dirty if the value has
been changed. When going from Fresh to Dirty, we charge the
gas cost the same as current scheme. A Dirty storage slot can be
reset back to Fresh via a SSTORE opcode. This will trigger a
refund.
When a storage slot remains at Dirty, we charge 200 gas. In this
case, we would also need to keep track of R_SCLEAR refunds -- if we
already issued the refund but it no longer applies (current value is
0), then removes this refund from the refund counter. If we didn't
issue the refund but it applies now (new value is 0), then adds this
refund to the refund counter. It is not possible where a refund is not
issued but we remove the refund in the above case, because all storage
slot starts with Fresh state.
State Transition
Below is a graph (by @Arachnid) showing possible state transition of gas costs. We ignore No-op state because that is trivial:
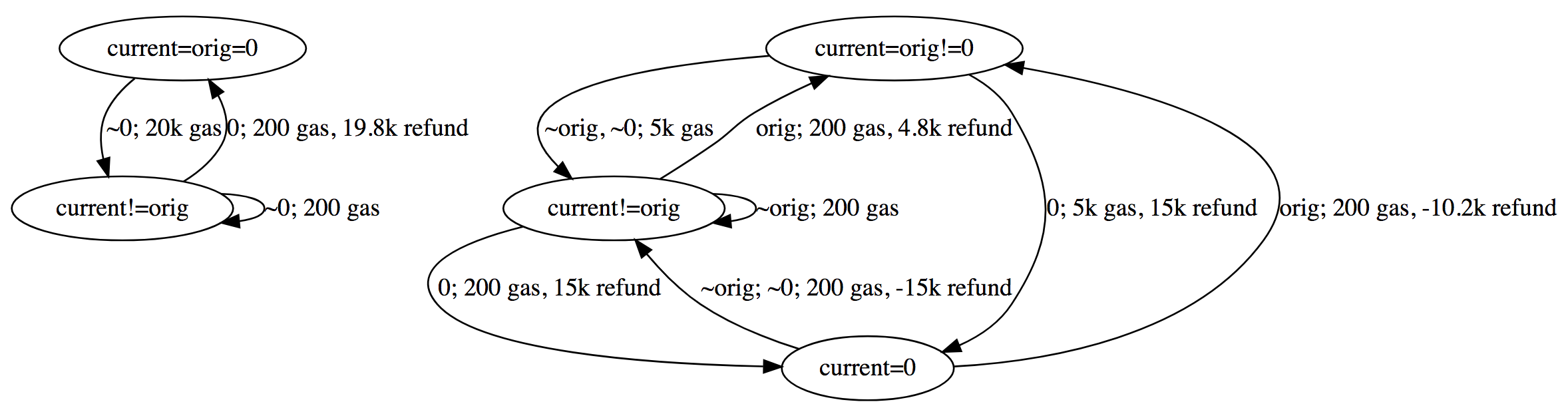
Below is table version of the above diagram. Vertical shows the new value being set, and horizontal shows the state of original value and current value.
When original value is 0:
A (current=orig=0) | B (current!=orig) | |
|---|---|---|
| ~0 | B; 20k gas | B; 200 gas |
| 0 | A; 200 gas | A; 200 gas, 19.8k refund |
When original value is not 0:
X (current=orig!=0) | Y (current!=orig) | Z (current=0) | |
|---|---|---|---|
orig | X; 200 gas | X; 200 gas, 4.8k refund | X; 200 gas, -10.2k refund |
~orig, ~0 | Y; 5k gas | Y; 200 gas | Y; 200 gas, -15k refund |
| 0 | Z; 5k gas, 15k refund | Z; 200 gas, 15k refund | Z; 200 gas |
Rationale
This EIP mostly achieves what a transient storage tries to do (EIP-1087 and EIP-1153), but without the complexity of introducing the concept of "dirty maps", or an extra storage struct.
- We don't suffer from the optimization limitation of EIP-1087. EIP-1087 requires keeping a dirty map for storage changes, and implicitly makes the assumption that a transaction's storage changes are committed to the storage trie at the end of a transaction. This works well for some implementations, but not for others. After EIP-658, an efficient storage cache implementation would probably use an in-memory trie (without RLP encoding/decoding) or other immutable data structures to keep track of storage changes, and only commit changes at the end of a block. For them, it is possible to know a storage's original value and current value, but it is not possible to iterate over all storage changes without incurring additional memory or processing costs.
- It never costs more gas compared with the current scheme.
- It covers all usages for a transient storage. Clients that are easy to implement EIP-1087 will also be easy to implement this specification. Some other clients might require a little bit extra refactoring on this. Nonetheless, no extra memory or processing cost is needed on runtime.
Regarding SSTORE gas cost and refunds, see Appendix for proofs of
properties that this EIP satisfies.
- For absolute gas used (that is, actual gas used minus refund), this EIP is equivalent to EIP-1087 for all cases.
- For one particular case, where a storage slot is changed, reset to its original value, and then changed again, EIP-1283 would move more gases to refund counter compared with EIP-1087.
Examine examples provided in EIP-1087's Motivation:
- If a contract with empty storage sets slot 0 to 1, then back to 0,
it will be charged
20000 + 200 - 19800 = 400gas. - A contract with empty storage that increments slot 0 5 times will be
charged
20000 + 5 * 200 = 21000gas. - A balance transfer from account A to account B followed by a
transfer from B to C, with all accounts having nonzero starting and
ending balances, it will cost
5000 * 3 + 200 - 4800 = 10400gas.
Backwards Compatibility
This EIP requires a hard fork to implement. No gas cost increase is anticipated, and many contracts will see gas reduction.
Test Cases
Below we provide 17 test cases. 15 of them covering consecutive two
SSTORE operations are based on work by
@chfast. Two additional
cases with three SSTORE operations is used to test the case when a
slot is reset and then set again.
| Code | Used Gas | Refund | Original | 1st | 2nd | 3rd |
|---|---|---|---|---|---|---|
0x60006000556000600055 | 412 | 0 | 0 | 0 | 0 | |
0x60006000556001600055 | 20212 | 0 | 0 | 0 | 1 | |
0x60016000556000600055 | 20212 | 19800 | 0 | 1 | 0 | |
0x60016000556002600055 | 20212 | 0 | 0 | 1 | 2 | |
0x60016000556001600055 | 20212 | 0 | 0 | 1 | 1 | |
0x60006000556000600055 | 5212 | 15000 | 1 | 0 | 0 | |
0x60006000556001600055 | 5212 | 4800 | 1 | 0 | 1 | |
0x60006000556002600055 | 5212 | 0 | 1 | 0 | 2 | |
0x60026000556000600055 | 5212 | 15000 | 1 | 2 | 0 | |
0x60026000556003600055 | 5212 | 0 | 1 | 2 | 3 | |
0x60026000556001600055 | 5212 | 4800 | 1 | 2 | 1 | |
0x60026000556002600055 | 5212 | 0 | 1 | 2 | 2 | |
0x60016000556000600055 | 5212 | 15000 | 1 | 1 | 0 | |
0x60016000556002600055 | 5212 | 0 | 1 | 1 | 2 | |
0x60016000556001600055 | 412 | 0 | 1 | 1 | 1 | |
0x600160005560006000556001600055 | 40218 | 19800 | 0 | 1 | 0 | 1 |
0x600060005560016000556000600055 | 10218 | 19800 | 1 | 0 | 1 | 0 |
Appendix: Proof
Because the storage slot's original value is defined as the value when a reversion happens on the current transaction, it's easy to see that call frames won't interfere SSTORE gas calculation. So although the below proof is discussed without call frames, it applies to all situations with call frames. We will discuss the case separately for original value being zero and not zero, and use induction to prove some properties of SSTORE gas cost.
Final value is the value of a particular storage slot at the end of
a transaction. Absolute gas used is the absolute value of gas used
minus refund. We use N to represent the total number of SSTORE
operations on a storage slot. For states discussed below, refer to
State Transition in Explanation section.
Original Value Being Zero
When original value is 0, we want to prove that:
- Case I: If the final value ends up still being 0, we want to charge
200 * Ngases, because no disk write is needed. - Case II: If the final value ends up being a non-zero value, we want to
charge
20000 + 200 * (N-1)gas, because it requires writing this slot to disk.
Base Case
We always start at state A. The first SSTORE can:
- Go to state A: 200 gas is deducted. We satisfy Case I because
200 * N == 200 * 1. - Go to state B: 20000 gas is deducted. We satisfy Case II because
20000 + 200 * (N-1) == 20000 + 200 * 0.
Inductive Step
- From A to A. The previous gas cost is
200 * (N-1). The current gas cost is200 + 200 * (N-1). It satisfy Case I. - From A to B. The previous gas cost is
200 * (N-1). The current gas cost is20000 + 200 * (N-1). It satisfy Case II. - From B to B. The previous gas cost is
20000 + 200 * (N-2). The current gas cost is200 + 20000 + 200 * (N-2). It satisfy Case II. - From B to A. The previous gas cost is
20000 + 200 * (N-2). The current gas cost is200 - 19800 + 20000 + 200 * (N-2). It satisfy Case I.
Original Value Not Being Zero
When original value is not 0, we want to prove that:
- Case I: If the final value ends up unchanged, we want to
charge
200 * Ngases, because no disk write is needed. - Case II: If the final value ends up being zero, we want to
charge
5000 - 15000 + 200 * (N-1)gas. Note that15000is the refund in actual definition. - Case III: If the final value ends up being a changed non-zero
value, we want to charge
5000 + 200 * (N-1)gas.
Base Case
We always start at state X. The first SSTORE can:
- Go to state X: 200 gas is deducted. We satisfy Case I because
200 * N == 200 * 1. - Go to state Y: 5000 gas is deducted. We satisfy Case III because
5000 + 200 * (N-1) == 5000 + 200 * 0. - Go to state Z: The absolute gas used is
5000 - 15000where 15000 is the refund. We satisfy Case II because5000 - 15000 + 200 * (N-1) == 5000 - 15000 + 200 * 0.
Inductive Step
- From X to X. The previous gas cost is
200 * (N-1). The current gas cost is200 + 200 * (N-1). It satisfy Case I. - From X to Y. The previous gas cost is
200 * (N-1). The current gas cost is5000 + 200 * (N-1). It satisfy Case III. - From X to Z. The previous gas cost is
200 * (N-1). The current absolute gas cost is5000 - 15000 + 200 * (N-1). It satisfy Case II. - From Y to X. The previous gas cost is
5000 + 200 * (N-2). The absolute current gas cost is200 - 4800 + 5000 + 200 * (N-2). It satisfy Case I. - From Y to Y. The previous gas cost is
5000 + 200 * (N-2). The current gas cost is200 + 5000 + 200 * (N-2). It satisfy Case III. - From Y to Z. The previous gas cost is
5000 + 200 * (N-2). The current absolute gas cost is200 - 15000 + 5000 + 200 * (N-2). It satisfy Case II. - From Z to X. The previous gas cost is
5000 - 15000 + 200 * (N-2). The current absolute gas cost is200 + 10200 + 5000 - 15000 + 200 * (N-2). It satisfy Case I. - From Z to Y. The previous gas cost is
5000 - 15000 + 200 * (N-2). The current absolute gas cost is200 + 15000 + 5000 - 15000 + 200 * (N-2). It satisfy Case III. - From Z to Z. The previous gas cost is
5000 - 15000 + 200 * (N-2). The current absolute gas cost is200 + 5000 - 15000 + 200 * (N-2). It satisfy Case II.
Copyright
Copyright and related rights waived via CC0.